Cadeia de Markov em apostas esportivas

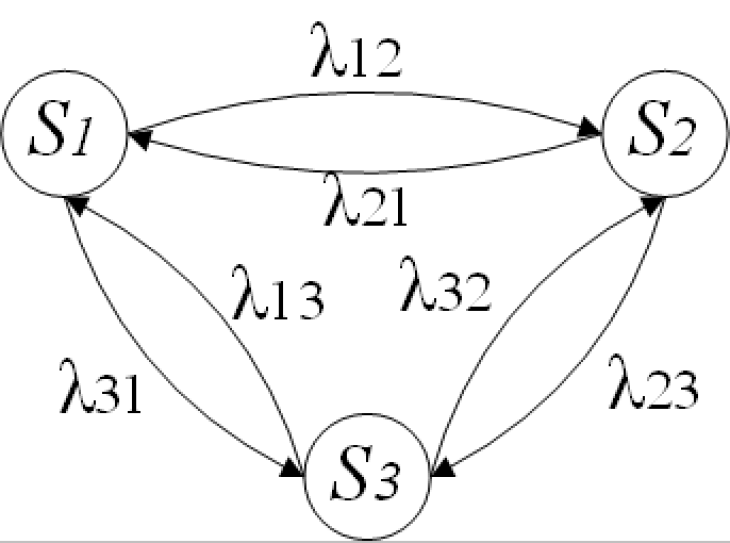
A cadeia de Markov (um processo aleatório discreto de Markov) é uma sequência de eventos aleatórios com um número finito de resultados possíveis, em que o futuro depende do estado atual, mas não depende do passado.

A cadeia de Markov ou, como também é chamada, o processo de Markov, ocupa um dos lugares centrais na teoria dos processos aleatórios. A teoria dos processos aleatórios é uma ciência que estuda os padrões dos fenômenos aleatórios na dinâmica de seu desenvolvimento.

Essa classe de processos aleatórios recebeu esse nome em homenagem ao matemático russo Andrei Andreevich Markov (1856-1922). Markov descobriu uma classe de processos estocásticos com componentes de tempo discretos e contínuos.

De acordo com Markov, a probabilidade de qualquer estado do sistema no futuro depende apenas do estado do sistema no momento, não dependendo de como o sistema chegou a esse estado.

Uma sequência aleatória de eventos é chamada de “cadeia de Markov” se cada transição de um estado para outro não depender de quando e como o sistema chegou ao estado atual. O estado inicial pode ser predeterminado ou aleatório.

O princípio da cadeia de Markov pode ser explicado por exemplo de uma cadeia de palavras. Por exemplo, em um texto com uma reportagem esportiva após a palavra “pênalti” é muito mais provável encontrar a palavra “remate” do que a palavra “batalhão”.

A cadeia de Markov é utilizada como um dos métodos de previsão em diversas áreas: econômica, social, política, financeira, na análise e processamento de texto e para outros fins. Por exemplo, cadeias de Markov são usadas em sistemas de digitação de texto como T9.